Procesos convencionales Sistemas aerobios

Sistema de lodos activos

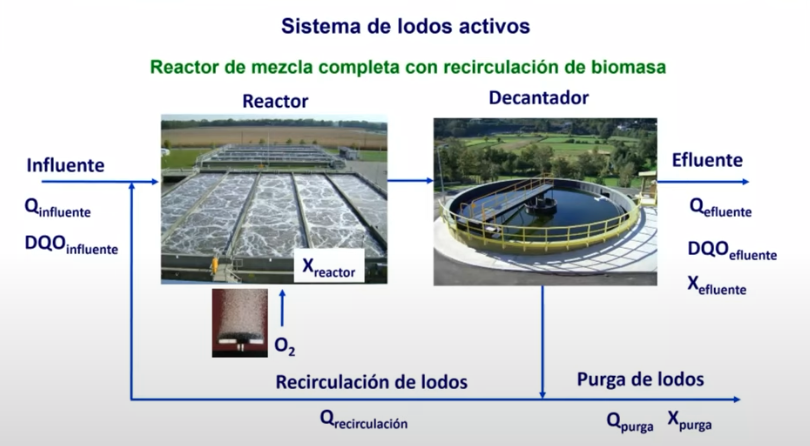
El sistema de lodos activos se puede representar mediante diferentes estructuras que se forman a partir de células libres mediante procesos de agregación:

Los lodos activos pueden presentarse en diferentes formas:

• Flóculos: Agregaciones de células microbianas
• Biopelículas: Pueden estar en suspensión o adheridas a un soporte fijo
• Gránulos: Formaciones esféricas de biomasa

Parámetros de operación y diseño

Tiempo de residencia hidráulico (TRH) en días

$$TRH = \frac{V_{reactor}}{Q_{influente}}$$

Tiempo de residencia de sólidos/celular (TRS) en días

$$TRS = \frac{V_{reactor} \cdot X_{reactor}}{Q_{purga} \cdot X_{purga} + Q_{efluente} \cdot X_{efluente}}$$

Eficacia del tratamiento en %

$$Eficacia = \frac{DQO_{influente} - DQO_{efluente}}{DQO_{influente}} \cdot 100$$

Carga orgánica en g DQO/día

$$CO = DQO_{influente} \cdot Q_{influente}$$

Velocidad de carga orgánica en g DQO/L*día

$$VCO = \frac{Q_{influente} \cdot DQO_{influente}}{V_{reactor}}$$

Velocidad de carga orgánica específica en g DQO/g SSV*día

$$VCO_{esp} = \frac{Q_{influente} \cdot DQO_{influente}}{V_{reactor} \cdot X_{reactor}}$$

Ejercicio 1

Tratamiento aerobio:

Un sistema aerobio de $2 m^3$ se alimenta a razón de $4 m^3/d$ con una agua residual que contiene $0.5 g DQO/L$. Si la concentración de biomasa es de $1.5 g SSV/L$ y la DQO de salida es de $80 mg DQO/L$, calcular:

1. Tiempo de residencia hidráulico (TRH)
2. Velocidad de carga orgánica (VCO)
3. Velocidad de carga orgánica específica (VCO_esp)
4. Carga orgánica (CO)
5. Eficacia del tratamiento

Si la concentración de biomasa en el efluente es de $30 mg SSV/L$ y de $5 g SSV/L$ en la corriente de recirculación de lodos al reactor. Calcular el caudal que se debe purgar de dicha corriente para que el tiempo de residencia celular (TRS) sea de $10 días$.

Velocidad de sedimentación

Ley de Stokes:

$$VSZ = \frac{g \cdot (\rho_{lodo} - \rho_{agua}) \cdot d^2}{18 \cdot \mu}$$

Donde:

• $g$: Aceleración de la gravedad ($9.81 m/s^2$)
• $\rho_{lodo}$: Densidad del lodo (kg/m³)
• $\rho_{agua}$: Densidad del agua (kg/m³)
• $d$: Diámetro de la partícula (m)
• $\mu$: Viscosidad del agua (Pa·s)

Flóculos:

• Tamaño: 10-150 μm --> Baja VSZ
• Densidad: 1020-1040 kg/m³

Índice volumétrico de lodos (IVL)

$$IVL = \frac{Vol_{30}}{X \cdot V_{total}}$$

Donde:

• $Vol_{30}$: Volumen lodo 30 minutos (mL)
• $X$: Concentración biomasa (g SST/L)
• $V_{total}$: Volumen de la probeta (L)

Buena sedimentabilidad: IVL < 150 mL/g SST

Dieta Floculos

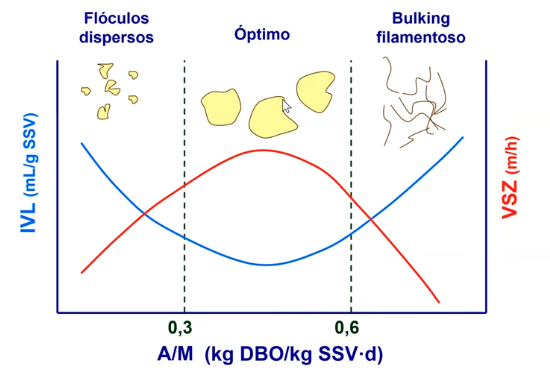
Influencia de la concentración de biomasa

La concentración de biomasa afecta significativamente los costos operativos:

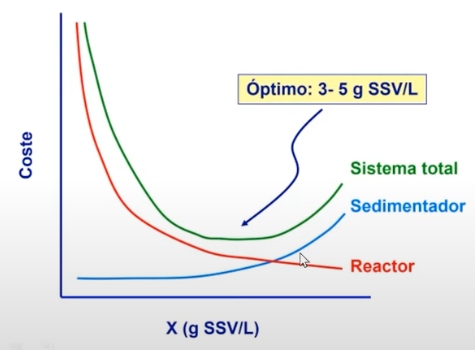
Puntos clave del gráfico:

• El punto óptimo de operación se encuentra entre 3-5 g SSV/L
• El costo total es la suma de los costos del reactor y sedimentador
• A bajas concentraciones, domina el costo del reactor
• A altas concentraciones, aumenta el costo del sedimentador

Cinética microbiana

Fases de crecimiento:

1. Fase de aclimatación
2. Fase de crecimiento exponencial
3. Fase estacionaria
4. Fase de muerte celular

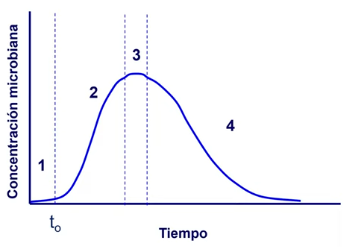
Fase 2: Crecimiento exponencial

Velocidad de crecimiento:

$$r_x = \frac{dX}{dt}$$

Donde:

• $X$: Concentración de biomasa (g SST/L)
• $r_x$: Velocidad de crecimiento (g SST/día)

Velocidad específica de crecimiento:

$$\mu = \frac{r_x}{X} = \frac{1}{X} \cdot \frac{dX}{dt}$$

$\mu \text{ cte} \rightarrow X = X_0 \cdot e^{\mu (t - t_0)}$

Tiempo de duplicación:

$$t_d = \frac{ln(2)}{\mu}$$

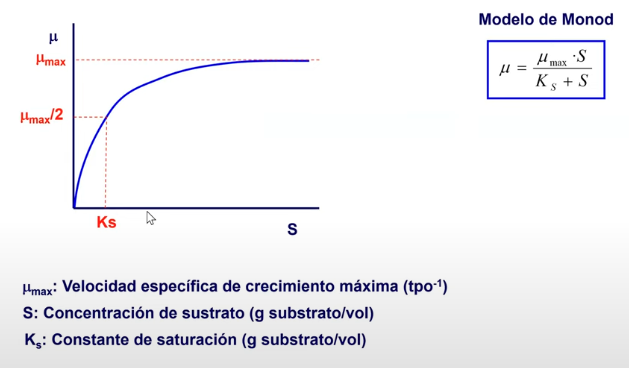
Modelo de Monod:

Fase 4: Muerte celular

Coeficiente de decaimiento:

$$k_d = \frac{dX}{dt} = -\mu \cdot X$$

Velocidad neta de crecimiento:

$$r'_x = \frac{\mu_{max} \cdot X \cdot S}{K_s + S} - k_d \cdot X$$

Velocidad especifica de crecimiento neto:

$$\mu' = \frac{\mu_{max} \cdot S}{K_s + S} - k_d$$

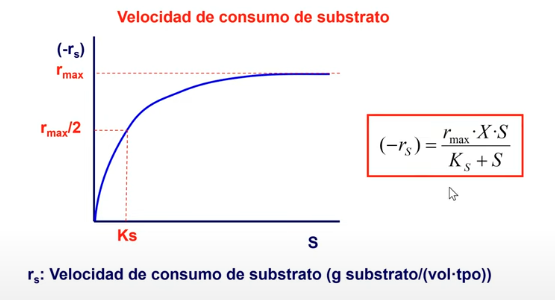
Velocidad de consumo de sustrato:

$$(-r_s) = \frac{r_{max} \cdot X \cdot S}{K_s + S}$$

Estequiometría microbiana

$\text{Microo + Sustratos} \rightarrow Y_{x/y} \cdot \text{Nuevos Microo} + Y_{p/s} \cdot \text{Productos Finales}$

Coeficientes de rendimiento:

• $Y_{x/y}$: Biomasa formada/substrato consumido
• $Y_{p/s}$: Productos formados/substrato consumido

$$r_x = Y_{x/y} \cdot (-r_s) = \frac{Y_{x/s}}{Y_{p/s}} \cdot r_p$$ $$Y_{x/s} = \frac{\mu_{max}}{r_{max}}$$

Balances de DQO

Características de la DQO:

Balance DQO: Estado estacionario

$$\text{Entrada = Salida (kg O}_2\text{/d)}$$ $$Q_0 \cdot DQO_0 - R_{O_2} = Q_{purga} \cdot DQO_{purga} + Q_{efluente} \cdot DQO_{efluente}$$

Donde:

• $Q_0$, $Q_{purga}$, $Q_{efluente}$: Caudal de entrada, purga y efluente (m³/d)
• $DQO_0$, $DQO_{purga}$, $DQO_{efluente}$: DQO de entrada, purga y efluente (kg O₂/m³)
• $R_{O_2}$: Requerimiento de oxígeno (kg O₂/d)

Requerimiento de oxígeno (R_O2)

El requerimiento de oxígeno en sistemas de lodos activos puede calcularse mediante la siguiente expresión:

$$R_{O_2} = Q_o \cdot (S_o - S) - (1.42) \left[ Q_e \cdot \frac{Y_{S/X} \cdot (S_o - S)}{1 + k_d \cdot TRS} + f_d \cdot k_d \cdot Q_e \cdot \frac{Y_{S/X} \cdot (S_o - S)}{1 + k_d \cdot TRS} \cdot TRS \right]$$

Donde:

• $R_{O_2}$: Requerimiento de oxígeno (kg O₂/d)
• $Q_o$: Caudal de entrada (m³/d)
• $S_o$: Concentración de DQO en el influente (kg O₂/m³)
• $S$: Concentración de DQO en el efluente (kg O₂/m³)
• $Y_{S/X}$: Coeficiente de rendimiento (kg SSV/kg DQO)
• $k_d$: Coeficiente de decaimiento (d⁻¹)
• $TRS$: Tiempo de residencia de sólidos (d)
• $f_d$: Fracción de biomasa que se transforma en productos residuales
• $1.42$: Factor de conversión de SSV a DQO (kg O₂/kg SSV)

Esta ecuación se compone de:

• DQO eliminada: $Q_o \cdot (S_o - S)$
• Biomasa generada: El término dentro del corchete que representa la DQO convertida en nueva biomasa

El balance entre estos componentes determina la cantidad de oxígeno necesaria para el proceso aerobio.